
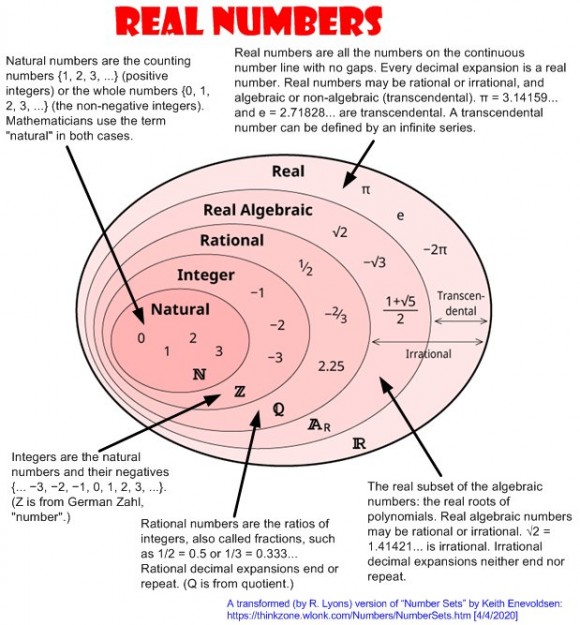
His notion of a computable real number is a real number that you can calculate as accurately as you may wish. What Turing says is that you calculate it with arbitrary precision. Actually, you never calculate it with infinite precision. But from an arithmetical point of view, if you want to calculate its numerical value digit by digit or bit by bit if you're using binary, it turns out that real numbers are problematical.Įven though to geometrical intuition points are the most natural and elementary thing you can imagine, if you want to actually calculate the value of a real number with infinite precision, you can get into big trouble. From the point of view of geometrical intuition a real number is something very simple: it is just a point on a line. So, if you just tell me exactly where a point is, that's a real number. And every point on this line corresponds to precisely one real number. If the point is all the way to the right, it's 1.0000. If it is all the way to the left in this unit interval, it's 0.0000.
So if I have a straight line one unit long, and I want to find out where a point is, that corresponds to a real number. What is a real number? It's just a measurement made with infinite precision. One of the important contributions of Turing's paper, not to computer technology but to pure mathematics, and even to philosophy and epistemology, is that Turing's paper distinguishes very clearly between real numbers that are computable and real numbers that are uncomputable. Computers don't quite measure up to the exalted standards of pure mathematics. This paper is called "On computable numbers, with an application to the Entscheidungsproblem." And what most people forget, and is the subject of my talk today, is that when Turing talks about computable numbers, he's talking about computable real numbers.īut when you work on a computer, the last thing on earth you're ever going to see is a real number, because a real number has an infinite number of digits of precision, and computers only have finite precision. This is Turing's famous 1936 paper in the Proceedings of the London Mathematical Society mathematicians proudly claim it creates the computer industry, which is not quite right of course.īut it does have the idea of a general-purpose computer and of hardware and software, and it is a wonderful paper. Let's start by going back to a famous paper by Turing in 1936. See the chapter on "Chaitin's Constant" in Finch (2003).īut as you will see, there are some strange things going on with the real numbers. There's even a real number - Ω - that has my name on it. I'm not trying to undermine what you may have learned in your mathematics classes. I will show you some really weird real numbers.

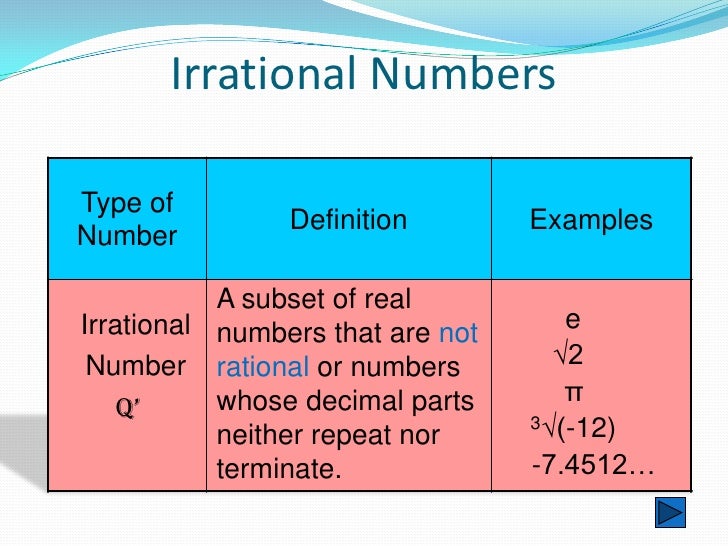
IBM Watson Research Center, Yorktown Heights, USA, Académie Internationale de Philosophie des Sciences, BELGIQUE, discuss mathematical and physical arguments against continuity and in favor of discreteness, with particular emphasis on the ideas of Émile Borel (1871-1956). Mathematics, Complexity and Philosophy to be published in a bilingual Spanish/English edition by Midas in Chile. More formally, a transcendental function is a function that cannot be constructed in a finite number of steps from the elementary functions and their inverses.Īn example of a Transcendental Function is the sine function sin(x).Dedicated to Newton da Costa on his 80th birthday.Īdapted from the second chapter of Chaitin's book In a similar way that a Transcendental Number is "not algebraic", so a Transcendental Function is also "not algebraic". The same argument applies to complex numbers. So there are many more Transcendentals than Algebraics.And since a Real number is either Algebraic or Transcendental, the Transcendentals must be "Uncountable".But the Real numbers are "Uncountable".The Algebraic Numbers are "countable" (put simply, the list of whole numbers is "countable", and we can arrange the algebraic numbers in a 1-to-1 manner with whole numbers, so they are also countable.).In fact, proving that a number is Transcendental is quite difficult, even though they are known to be very common. Then in 1882, Ferdinand von Lindemann proved that π ( pi) is transcendental. It took until 1873 for the first "non-constructed" number to be proved as transcendental when Charles Hermite proved that e ( Euler's number) is transcendental. and is in the class of Liouville Numbers. That number is now known as the Liouville Constant. In fact, Joseph Liouville had successfully made the first provable Transcendental Number. it is not the root of any polynomial equation and so is not algebraic.(the digit is 1 if it is k! places after the decimal, and 0 otherwise.) They transcend the power of algebraic methods.īack in 1844, Joseph Liouville came up with this number:


 0 kommentar(er)
0 kommentar(er)
